
In linear systems, responses to stimuli are proportionate. Nonlinear systems do not give proportionate responses. A quintessential example of a nonlinear system is Earth's atmospheric climate. If you put more energy into it, it produces disproportionately extreme weather. We will see more evidence of this during your lifetime. There will be more hurricanes and more evil winter storms.
Newton's gravity theory is linear and therefore obeys a superposition principle: to find the gravitational field of multiple bodies, you simply add up the gravity fields of the individual bodies. But Einstein's gravity theory is nonlinear. It has inherently different properties as a physical theory and describes a much richer range of phenomena. Black holes appear as mathematical solutions of the Einstein equations, and they rely on the nonlinearity of GR.
(This is an advanced point, but you can even have black holes happening when there is no matter around: it is the gravity itself that provides the effective mass. Quite surprising!)
The picture below gives a schematic diagram of the anatomy of a black hole. As we know, the event horizon is the surface of no return. It hides everything that falls across it from outside observers. The singularity is at the centre of the black hole and is where spacetime curvature and tidal forces become infinite. This is a puzzling flaw of Einstein's GR, about which we will have much more to say later this semester. Stay tuned!

We mentioned in our Time Dilation and Twin Paradox class that Einstein is a rock star among physicists partly because he pioneered the idea of a Gedankenexperiment. Astronomers make increasingly exquisite measurements of properties of black holes and other astronomical objects, but they cannot do active experiments on black holes. This is where the Gedankenexperiment comes in handy: we imagine doing experiments like throwing graduate students into black holes. Obviously, this is not something we would even consider doing in real life.
In four dimensions of spacetime - ours - there is a theorem (mathematically bulletproof statement) that black holes cannot support any kind of frills or bling - they have no hair. What this means conceptually is that, from the outside, a stationary black hole can be distinguished by only three characteristics: mass $M$, angular momentum $J$, and charge $Q$. Black holes in the real universe cannot carry macroscopic charge, because there is a mechanism (called the Schwinger mechanism) that discharges the charge $Q$ very quickly. So astrophysicists only talk about black holes with $M$ and $J$. But black holes can carry more exotic types of charge than the ones in the Standard Model, and studying how that plays into the mathematical theory has proven to be very helpful in the last eighteen years or so especially. By the way, it is no accident that these three properties of black holes sound the same as the three subatomic particle invariants - mass, spin and charge. The mass, angular momentum and charge of a black hole are properties of the whole spacetime. They prescribe how strongly gravitational and electromagnetic fields fall off with distance away from the centre of the black hole. They are strongly integrated with the physics of the horizon and the singularity.
Stephen Hawking is one of the 20th/21st Century's greatest theoretical physicists. He is also an incredible human being who gets on with the joy of doing theoretical physics research while having one of the world's most restrictive physical disabilities. He provides me and many others with tremendous amounts of inspiration. I was lucky enough to be invited to his 60th and 70th birthday conferences in Cambridge at DAMTP.
Hawking is famous because he realized that quantum mechanics, the physics of the very small, is actually relevant to the physics of black holes and that black holes emit radiation! This was a tremendous surprise to his colleagues thinking about the mathematical physics of gravity at the time. His radiation, known as Hawking radiation, gave rise to a puzzle that I and other physicists are still working on forty years later, known as the Black Hole Information Paradox. More on that shortly.
Hawking discovered that black holes emit radiation at a temperature $$ T_H = {\frac{\hbar c^3}{8\pi G_N k_B M}} \,. $$
For an astrophysical black hole, this Hawking Temperature is unmeasurably cold. For example, for a stellar mass black hole the luminosity of the Hawking radiation from a black hole would be only $10^{-28}$ Watts. There are two really interesting things about the Hawking temperature formula. One is that it involves four physical constants - Planck's constant $\hbar$ from quantum mechanics, the speed of light $c$ from relativity, Newton's gravitational constant $G_N$, and Boltzmann's constant $k_B$ of thermodynamics. So Hawking radiation is a quantum relativistic gravitational thermodynamic phenomenon (phew, that was a mouthful!). The other interesting thing is that the Hawking temperature depends inversely on the mass. This means that smaller black holes are fiercer: they have a higher Hawking temperature.
In order to calculate this black hole temperature, Hawking had to bring to bear two major theoretical methods from 20th century physics: GR and Quantum Field Theory (QFT). QFT is what you get when you put Quantum Mechanics (to be introduced next week) together with Einstein's Special Relativity. QFT describes the quantum physics of subatomic particles at high energies relevant to the LHC and Big Bang. So Hawking's calculation was pretty heavy on the math.
What Hawking radiation implies is something pretty spectacular: left to their own devices, black holes evaporate! Furthermore, when they have evaporated down to really small size they get really fierce. The end of their life must be a pretty fascinating process - and physicists like me are busily researching how to find these answers. We are definitely not there yet, but string theorists have made partial progress. Astrophysical black holes are so large that their lifetime is orders of magnitude greater than the age of the universe, so we do not have to worry about that happening to the black hole at the centre of our galaxy or to Cygnus X-1. The small violent primordial ones are the fascinating ones for people like me.
The idea of Hawking radiation is something pretty amazing to behold. Black holes can leak radiation - photons for example. So does that mean that something can get out of a black hole after all? Does this mean we can eventually rescue things that fell in somehow? Or not? To make progress towards answering these questions we will need to delve more deeply into how Hawking radiation can happen in the first place.
We already met antiparticles in our seminar on the Standard Model of Particle Physics. What we did not talk about then is that the `vacuum' is actually a very active place. Virtual particle-antiparticle pairs actually pop in and out of existence probabilistically, for very short periods. They are called virtual particles (and antiparticles) because they can only live for an extremely short time allowed by the Heisenberg Uncertainty Principle of quantum mechanics. It is as if you are allowed to commit the sin of creating a particle-antiparticle pair out of nothing if you do the crime so quickly that noone notices.
For instance, a virtual electron-positron pair can live for only about $10^{-21}$ seconds. The fleeting appearance of a virtual particle-antiparticle pair is depicted in cartoon style below. If virtual particles are to turn into real particles, someone has to give them energy. Otherwise their fleeting existence comes to an end and they vanish back into the vacuum from where they came.
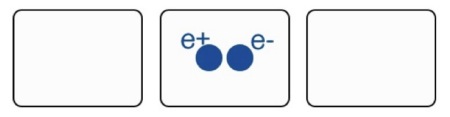
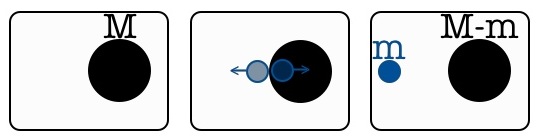
For the purposes of explaining Hawking radiation, virtual pairs created wholly outside the horizon are boring and so are virtual pairs created wholly inside the horizon. The interesting virtual pairs are the ones that straddle the black hole horizon. For straddler pairs, the virtual particle outside the horizon can, if it has enough momentum, escape out to infinity. To do this, it has to steal a little bit of mass-energy from the black hole to become a real particle (rather than a Pinocchio particle). Accordingly, the black hole loses a little mass-energy by emitting Hawking radiation. This is why we say Hawking radiation makes black holes evaporate slowly. But what about the virtual particle, the antiparticle of the escapee, who is in prison behind the horizon? He never makes it. He gets absorbed back into the black hole interior.
In the 19th century, physicists invented a set of ideas to describe the thermal behaviour of things like gases, liquids and solids. They were motivated by trying to figure out how to efficiently convert heat (like in a fire) into work (like pushing a cart down the street). Thermodynamic variables describe gross properties of stuff, like temperature and pressure. Talking about gross properties is a smart way to describe gases, because it is a whale of a lot easier than tracking the individual motions of each atom or molecule making up the gas!
In the golden era of development of thermodynamic theory, the concept of entropy was invented. Entropy encodes the amount of energy that is wasted as heat in a thermodynamic process - for instance, the waste heat that is emitted out the tailpipe of a motor vehicle running on a gasoline-powered internal combustion engine. If there is a lot of entropy per power stroke, that means our engine is not very efficient. Entropy plays another related role: it encodes the degree of disorganization of a physical system. For example, a tidy dorm room would have low entropy while a messy dorm room would have high entropy.
Entropy, and other thermodynamic concepts of real value for macroscopic systems, can be explained from a more fundamental (more microscopic) point of view using knowledge of the quantum mechanics of individual particles. For instance, if I am clever enough to understand the quantum mechanics of one hydrogen molecule, then I can use that knowledge to figure out the entropy of a box of hydrogen gas containing bazillions of hydrogen molecules. Pretty cool, huh? The guy who worked this out first and has his name on a Law is Ludwig Boltzmann. He found that the entropy of the system $S$ could be calculated from the number of ways $W$ that the system could be configured by taking the natural logarithm and multiplying by what in modern times we call the Boltzmann constant $k_B$, $$ S= k_B \ln(W) \,. $$ Boltzmann was so in love with his discovery he had it engraved on his tombstone. I mean, OMG!
You already know the First Law of Thermodynamics: energy is neither created nor destroyed but instead transferred from one form to another. The Second Law of Thermodynamics is even more important; it says that in general the total entropy of a closed system (something that has neither matter nor energy flowing in/out of its boundaries) never decreases with time. Said another way, a closed system naturally tends to become more disorganized with time. This is no excuse for the state of teenage bedrooms, however! The Second Law says that if you make part of a closed system less entropic, that has to come at the cost of at least as much increased entropy somewhere else. So when Mum tidies the messy teen's bedroom, the entropy of his room decreases but it is not a closed system: Mum intervened. Earth is not a closed system either: it receives energy and particles from the Sun, solar system, and outer space.
There are many equivalent forms of the Second Law, but the most relatable is probably the one that says that there is no such thing as a free lunch. Another way of saying it is that there is no such thing as a perpetuum mobile (perpetual motion machine): in any physical process converting heat into work, some heat is always wasted. You can build the most efficient engine on Earth and it still will not come anywhere close to violating the Second Law of Thermodynamics. It does not matter how inventive or imaginative or brilliant you are, you still cannot beat the Second Law. It is so bulletproof that I would personally bet my life and the lives of my living and future relatives on it.
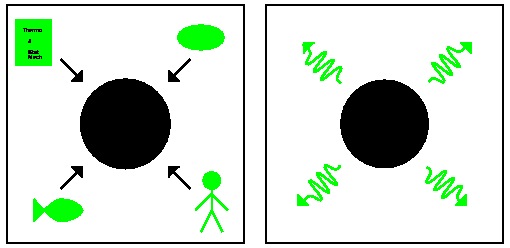
After Stephen Hawking made his momentous discovery that black holes radiate, everyone interested in black hole physics developed a burning curiosity (pun intended) about black hole thermodynamics. Jacob Bekenstein first figured out the physics of black hole entropy. Accordingly, the formula for black hole entropy is known as the Bekenstein-Hawking formula. The entropy of the black hole is thought to encode information about the many different ways the black hole could have been formed, as shown below.
As you might suspect by now, this black hole entropy depends only on its mass, angular momentum, and charge. The Bekenstein-Hawking entropy is given by one-quarter of the area of the black hole horizon, measured in units of the Planck length $\ell_P$, $$ S_{BH} = {\frac{A}{4 \ell_P^{2}}} \,. $$
The most amazing thing about black hole entropy is how huge it is. The numerical value for the entropy of the black hole at the centre of our galaxy, for example, is about $10^{90}$. This happens to be approximately the total number of protons in the visible universe. Black holes are actually the most information-dense objects known. There is nothing capable of holding so much information as a black hole. But if someone will try to sell you a cloud storage plan based on black holes, say No thanks!
because you know you will never see the information again.
Gravitational string theorists like me would love nothing more than to explain from quantum gravity how the black hole entropy comes about. We have done this since 1996 using tools from string theory for special restricted classes of black holes that do not occur astrophysically. People will be really impressed once we finally figure out how to calculate the entropy of astrophysical black holes from first principles with no hand-waving. Once we manage to do this honestly, we will be able to solve the Black Hole Information Paradox. We will know how information falling into black holes eventually comes out again as subtle correlations in the outgoing Hawking radiation.